Python : Day 15 – Lesson 15

Processing steps in seq2seq model

Now, let's think about the processing steps in seq2seq model.The feature seq2seq model is that it consists of the two processes:

1. The process that generates the fixed size vecor z from the input sequence X.

2. The process that generates the output sequence Y from z.

In other words, the information of X is coveyed by z and 𝑃𝜃 (𝑦 𝑗|𝑌< 𝑗, 𝑋) is actually calculated as 𝑃𝜃 (𝑦𝑗|𝑌𝑗, 𝑧).

First we represent the process which generating z from X by the function Λ.

The function Λ may be the recurrent neural net such as LSTMs.

Second, we represent the process which generating Y from z by the following formula:

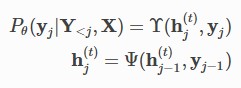
𝑗

Ψ is the function to generate the hidden vectors ℎ(𝑡), and Υ is the function to calculate the

𝑗−1

generative probability of the one-hot vector 𝑦𝑗 . When j=1, ℎ𝑡

or ℎ𝑡

is z generated by

0

Λ(𝑋), and y_{j-1} or 𝑦0 is the one-hot vector of BOS.

Model architecture of seq2seq Model

Now, we will discuss about the architecture of seq2seq model.To ease in explanation, we used the most basic architecture. The architecture of seq2seq model can be seperated to the five major roles.

1. Encoder embedding layer

2. Encoder Recurrent layer

3. Decoder embedding layer

4. Decoder Recurrent layer

5. Decoder Output layer

The encoder consist of two layers: the embedding layer and the recurrent layer, and the decoder consist of three layers: the embedding layer, recurrent layer and output layer.

In explanation, we use the following symbols:

1. Encoder embedding layer

   
   

   The first layer or encoder embedding layer converts each word in input sentence to the embedding vector. When processing the i-th word in the input sentence, the input and output of the layer are the following:

   
   

   The input is 𝑥𝑖 : the one-hot vector which represents the i-th word.

   The output is 𝑥𝑖 : the embedding vector which represents the i-th word.

   Each embedding vector is calculated by this equation: 𝑥𝑖 = 𝐸(𝑠) 𝑥𝑖

   
   

   𝐸(𝑠)

   (𝑠)

   𝐷𝑥𝜈

   ∈ \R is the embedding matrix of the encoder.

   
   

2. Encoder recurrent layer

   
   

   The encoder recurrent layer generates a hidden vectors from the embedding vectors. When we processing the i-th embedding vector, the input and output layer are the following:

   
   

   𝑖

   The input is 𝑥𝑖 : the embedding vector which represents the i-th word. The output vector is ℎ(𝑠 ) : hidden vector of the i-th position

   
   

   For example, when using the uni-directional RNN of one layer, the process can be represented as the following function Ψ(𝑠) :

   
   

   
   

   In this case, we have used tanh as the activation function.

   
   

3. Decoder Embedding layer

   
   

   The decoder embedding layer converts each word in the output sentence to the embedding vector. When processing the j-th word in the output sentence, the input and output layer are the following:

   
   

   The input is 𝑦𝑗−1 : the one-hot vector which represents the (j - 1)-th word generated by the decoder output layer.

   𝑗 −

   The output is 𝑦𝑗 : the embedding vector which represents the (j - 1)-th word. Each embedding vector is calculated by the following equation: 𝑦 = 𝐸(𝑡) 𝑦𝑗 1

   **𝐸𝑡

   𝐷𝑥|𝜈(𝑡)

   \R

   ∈

   is the embedding matrix of the encoder.

   
   

4. Decoder Recurrent layer

The decoder recurrent layer generates the hidden vectors from the embedding vectors. When processing the j-th embedding vector, the input and the output layers are following:

In [ ]: